矩阵相乘的法则为什么是现在这样
来源:从书本上学到的 2022-02-19 math
学过线性代数的人,都会矩阵相乘。那矩阵相乘背后的道理是什么呢?
大约在1855年,Cayley(英国数学家,矩阵理论的先驱)在研究线性方程的复合问题时,提出了矩阵相乘的法则。基本过程如下:
假设有两个线性系统f(x)、g(x)如下:
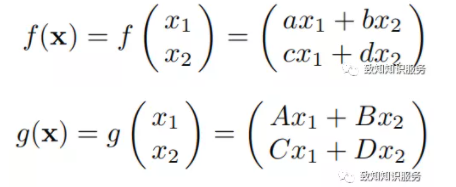
其中,f(x)是由两个线性表达式构成的线性系统,g(x)也是如此。
那么,若有线性系统h(x)是f(x)和g(x)的复合系统,则有
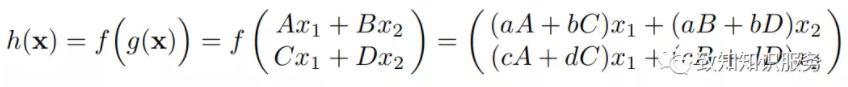
把三个线性系统的系数用如下矩阵形式表示出来,
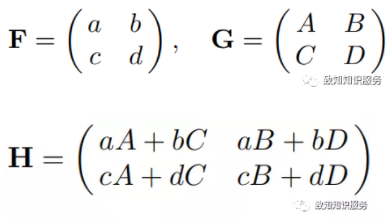
根据变量前面的系数的对应关系有,
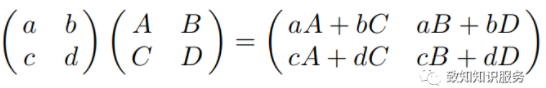
上式就是我们现在所用的矩阵乘法法则。
Cayley称H是F和G的复合(composition)或乘积(product),换句话说,矩阵相乘法则源于线性系统的复合,其含义也是表示了线性系统的复合。
简单地说,线性系统的线性系统仍是一个线性系统。
这就是矩阵乘法的由来和含义。从中也能窥见一些线性代数中“线性”二字的意涵。
- END -
热门推荐
- 从实例认识大数据 2023-10-16
- 业务流程再造 2023-09-04
- 优化方法发展现状 2023-03-27
- 优化方法的“三板斧” 2022-10-04
- 容许区间与置信区间 2022-07-19
- 概率密度函数中形状参数和尺度参数 2022-07-19
- 天下没有免费的午餐 2022-04-24
- 抽签问题 2022-03-23
- 发帖规则 2022-02-23
- 信度和效度 2022-02-20
- 为什么变量总是X,Y,Z 2022-02-20
-
 取消
取消
 收藏
收藏
-
 打赏
打赏
-
 评论
评论
-
返回
顶部




{{item1.comment_time | formatDate}}
{{item1.comment_text}}